
Beginners guide to CAD data
Prepare your business for Industry 4.0, learning how 3D data is presented in CAD.
Get the guide
Beginners guide to CAD data
Prepare your business for Industry 4.0, learning how 3D data is presented in CAD.
Get the guidePrecise geometry and tessellation. B-Reps and meshes.
As discussed in part 2, B-Rep (Boundary Representation) and polygonal (mesh) are two key types of representations used in CAD. Let’s consider each one in more details. The former is used to describe precise (exact) geometry whereas the latter – approximated or tessellated one.
B-Rep defines a 3D body via set of geometrical entities (points, curves, and surfaces) and topological entities (vertices, edges, faces, shell, solid). The former provides geometrical definition of the body boundary (e.g. a ship hull surface, car body, etc) whereas the latter trims the geometry (which can be infinite in theory) and stores connectivity information.
B-Rep allows to “precisely” define a 3D body, i.e. to describe its boundary using precise geometrical definitions. That is, if you model a car body or a kettle in your favorite CAD system, then you deal with B-Rep definition under the hood.
B-Rep bodies are classified into:
- Solid body – represents a lump of material in 3D space. Examples of a solid body can be a bolt, a piston, a gear or alike. Something which is manufactured using machining (milling, drilling), forging, casting and other processes.
- Sheet body – a (relatively) thin surface-like body in 3D space. Think of a car body element or a ship hull. Something which is manufactured using molding or bending.
- Wireframe body – a wire-like body in 3D space. Mainly used as simplification of a body in real-world (e.g. electrical wires).
- Acorn body – basically a single vertex in 3D space. Again, rather simplification of a a real-world body when precise shape is not important.

One of the future series will dive into more details on B-Rep’s geometry and topology to provide in-depth understanding of which data B-Rep uses to describe bodies.
Which modeling techniques are used to design a B-Rep body? The list can be quite long and often depends on the capabilities of the CAD system and of the underlying geometrical kernel. They can include (the list is not meant to be exhaustive):
Solid modeling:
- 2D sketching followed by extrusion and rotation
- Using solid primitives (such as box, sphere, torus, cone, cylinder)
- Boolean operations (cut, fuse, common)
- Fillets and chamfers
- Offsetting and hollowing
- Sweeping
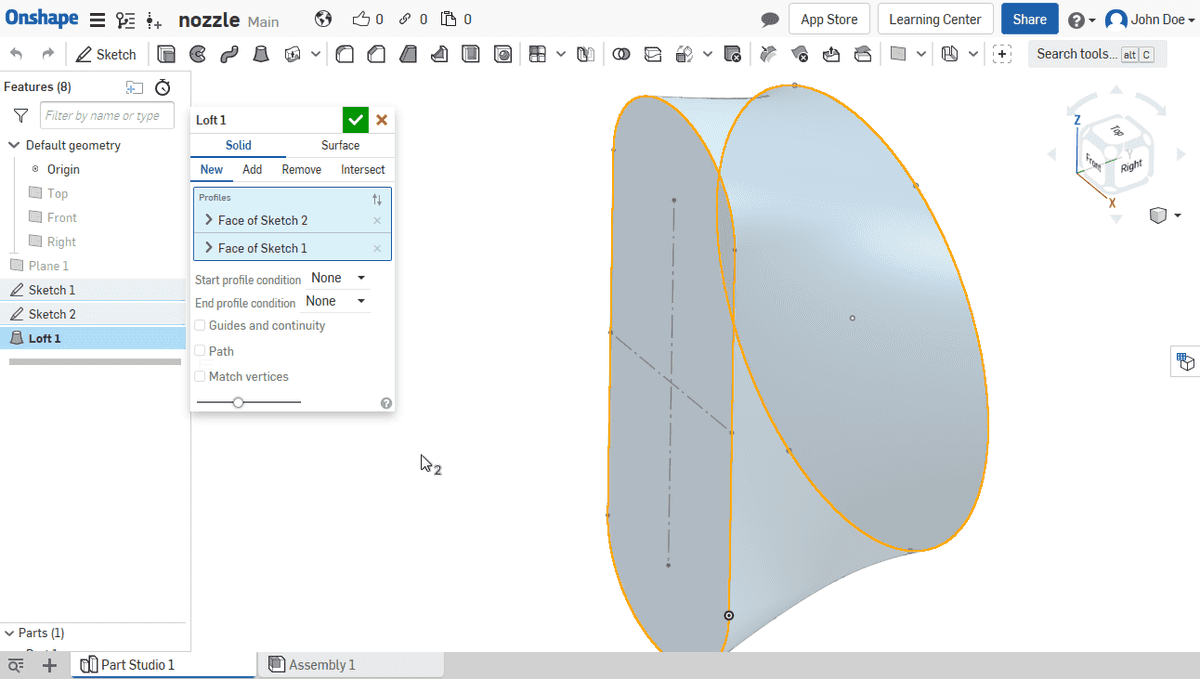
- Lofting
Sheet modeling:
- Extrusions and rotations (extruding/rotating an edge will give you a face; a wire will give you a shell)
- Offsetting
- Sweeping and lofting
Gallery
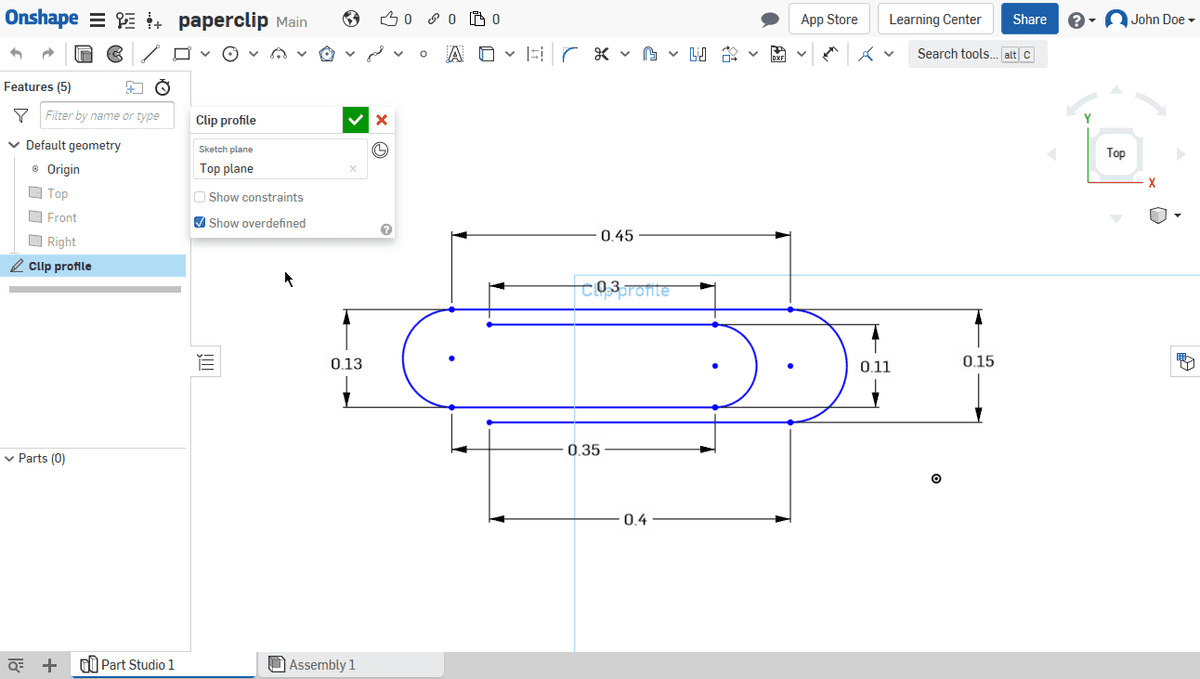
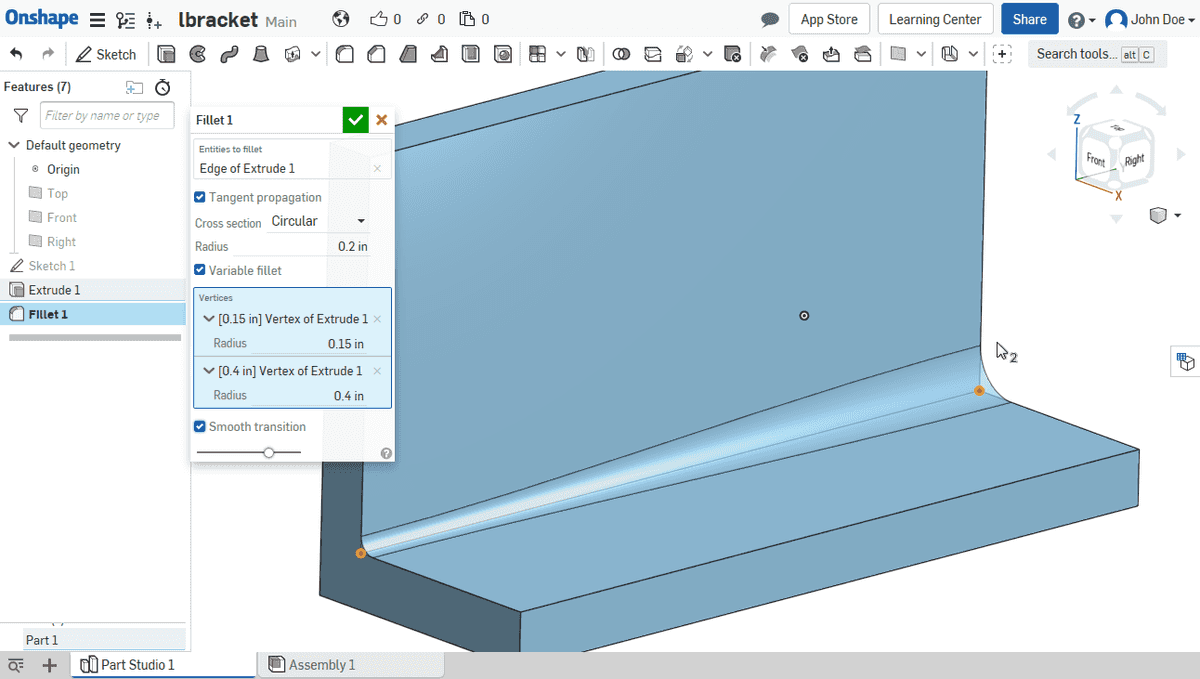
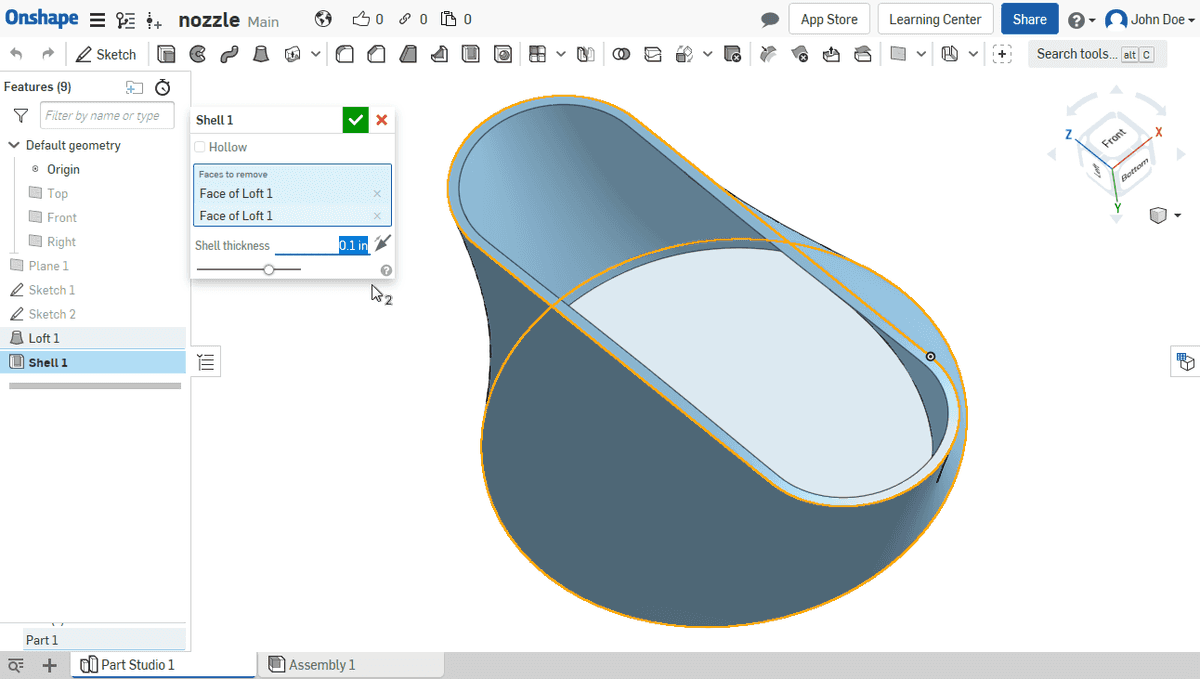
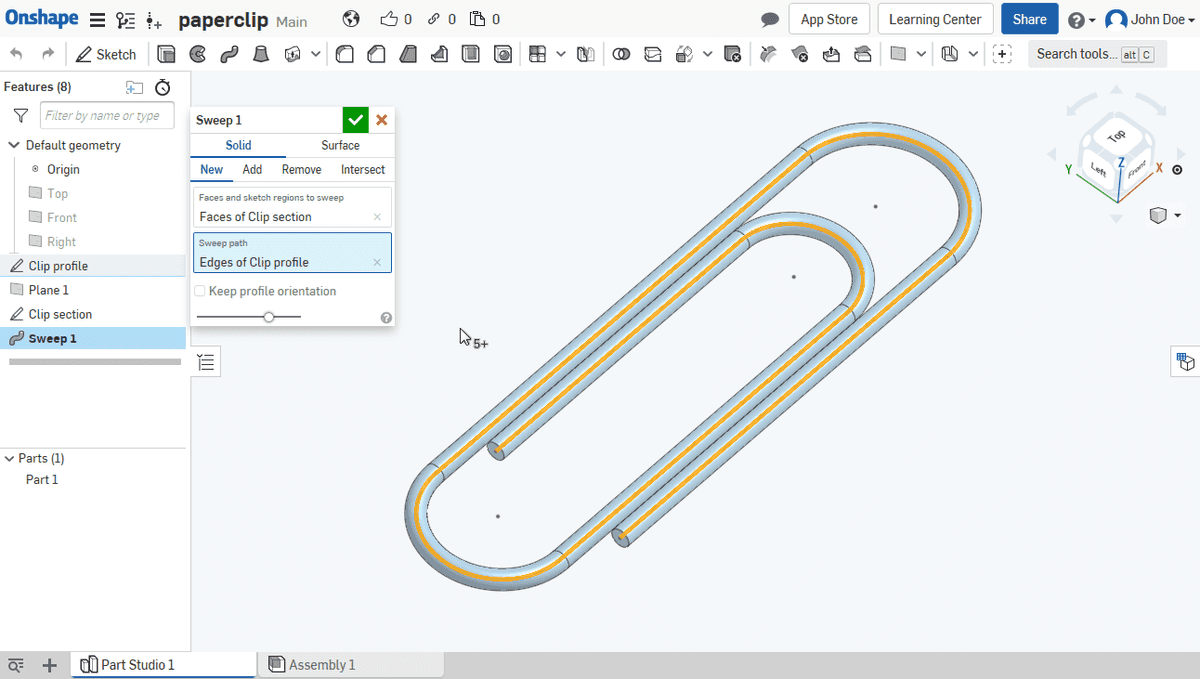
Meanwhile let’s jump to the meshes which are often used in replace of (or in conjunction with) B-Reps.
Why would B-Rep’s not be sufficient? If B-Rep conveys precise information why would we need anything else? Why would meshes be so popular?
There are two key driving factors:
- Dealing with B-Rep is compute-intensive (e.g. computing a point on a B-Spline surface can take 100x-1000x machine operations comparing to computing a point on a planar triangle).
- Precise B-Rep definition is not always available. For instance, in reverse-engineering workflows such as 3D scanning (e.g. in dental industry, digital twins / equipment inspection and so on).
So meshes are used as approximated (linearized) 3D model where each precise boundary (face-on-surface and edge-on-curve) is replaced with a set of facets (triangles and linear segments).
Meshes are directly used in CAD not only to represent a B-Rep-less 3D model (or as an additional representation) but to display a 3D model on the screen. When you see a B-Rep body in a 3D view you essentially see its polygonal twin (as OpenGL, WebGL or other technologies use tessellated representation to feed into the graphic card).
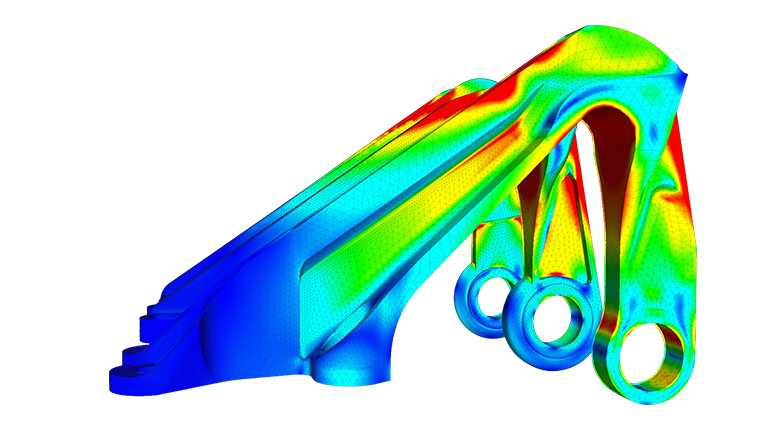
Meshes are used in CAE (Computer-Aided Engineering), applying Finite-Element Methods (FEM) in particular. They involve heavy-weight computations by solving partial differential equations on large meshes in domains of structural analysis, Computer Fluid Dynamics (CFD), heat transfer or electromagnetism.
Meshes can also be used in CAM (Computer-Aided Machining) for collision detection, tool-path generation and other scenarios.
For the last few years, B-Rep and mesh modeling start to co-exist in CAD scenarios in the frames of so called convergent modeling (announced for Parasolid and ACIS kernels). However truth to be told, we don’t have real-world examples of such models in our test data base yet (although we have dozens of thousands of Parasolid and ACIS in our test environment).
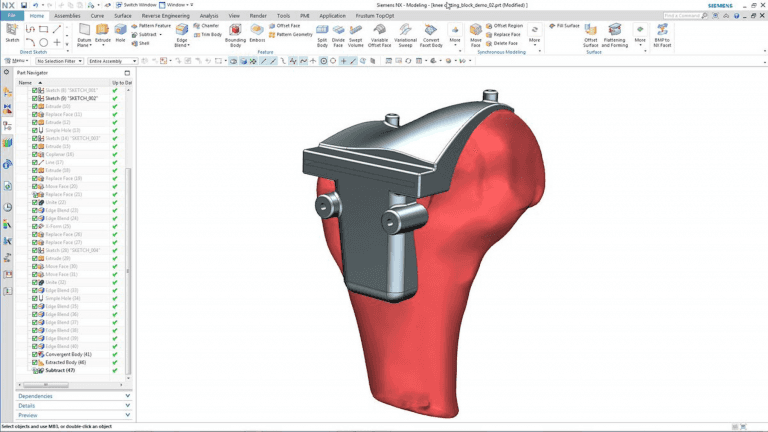
(image from design-engineering.com)
Obviously, for the same B-Rep body, multiple polygonal representations can be generated. The resulting mesh is determined by the mesh generator: the parameters it accepts (such as chordal and angular deviations, min/max size elements, aspect ratio, growth factors, etc), and the trade-offs it makes (quality/speed/mesh size, etc). Some meshes are tailored for visualization purposes (to produce a decent visual look using a minimum amount of triangles and running at the highest speed). Some favor quality to enable stable FEM execution at the expense of speed.

Depending on a workflow these multiple meshes generated for the same B-Rep need to be stored all together. For instance, a nut in a large aircraft can be tessellated with coarser settings to be displayed in the context of the entire aircraft (as it may be not seen after all, so there is no point in storing all the triangles). The same nut however needs to be displayed with fine details when it is zoomed in and displayed alone on screen. In that case the nut model may need to store an original B-Rep and a few meshes to be used for visualization. This concept is called Levels of Details (LOD) and will be addressed in the future posts.
By now, it should be clearly seen that generating a polygonal representation from B-Rep one is straightforward, whereas the other way around (from polygonal to B-Rep) is nearly impossible. Although you may achieve certain good degree of reconstruction (e.g. by recognizing elementary geometries such as planes or cylindrical holes), in a general case it is just an approximation at best. Some time ago we wrote a blog post explaining that challenge and recommend reading it to non-CAD professionals who approach with STL-to-STEP or alike inquiries. We don’t give up this topic of mesh-to-BRep conversion though and have it in our product backlog.
OK, this post was quite full of information so let’s stop here and continue next time.
Related readings:
Everything you need to know about CAD file formats
Next parts:
Part 4. CAD model structure. Parts and assemblies